| 楕円の代数定義は次の2次関数である。a = bで半径aの円になる。 曲線の表示で便利なのは極座標表示。楕円は次のｘ 、ｙ のセットで表現できる。 これが楕円曲線であることは、最初の式に代入して、次の定理を適用して確認できる。 曲線の極座標表示は便利で、長さを角度φの関数とすると色んな曲線が表現できる。 以上は曲線のパラメトリック表現で、パラメトリとして角度を採用 した訳だが、この場合の角度は物理的には経度、緯度といった意味ではない。円の場合はいいのだが、φ＝45度で楕円の1/4点とは対応しない。測量計算には不向きな表現だ。 地球表面と地球中心からの距離を r とし、緯度φで極座標表示すると次ぎの式となる。 最初の式を満足しなければならないのでｒ (φ）が決まる。 |
| 楕円を描くとき、どうしますか。ＣＡＤでは、中心、長円端、短円端を指示すれば終りです。江戸時代、職人さんはどうしていたのだろう。 半径500の円を描くときは、紐を二つに折って500のところで結ぶ。結んだ紐を中心の釘 に掛け、先の筆を力いっぱい回す。円が描ける。 楕円の時は、中心の釘の両脇に釘を打ち、同じことをした。それで扁平な円が描ける 。楕円の定義そのものを、職人さんは経験で知っていたのだろう。 石工の棟梁は自由に形を操らなければならない。長円を500として、短円を400にする には釘を300に打ち、紐を800で結ぶ。経験を整理して持っていたのだろう。 現場で使う金尺に、その組み合わせが目盛ってあった。と、想像するのだが。  熊本に、石匠館という石工の博物館がある。そこには金尺が展示されていた。 もう一度じっくり見てみたいと思っている。 |
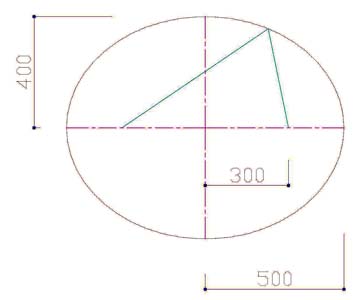
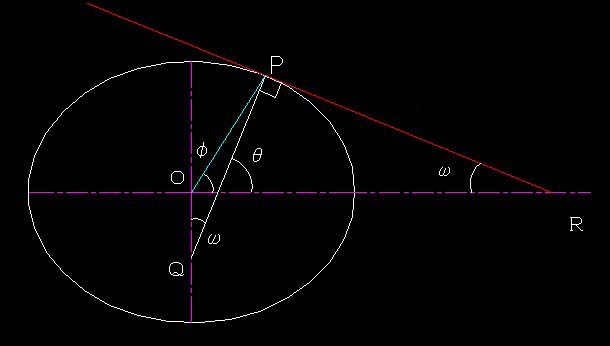
| 2点からの距離の合計が一定な曲線を楕円と呼ぶ。 長半径a,短半径ｂ、楕円中心から焦点までの距離ｃとすると、 この楕円のある点に接線を引く。職人さんはどうしたろうか。 多分、棟梁は焦点との角度を測らせた。180からその角度を引き、半分 を両脇に割り振り、その点を結ばせた。と想像する。 熊本に通潤橋というりっぱな石橋がある。江戸末期に完成している。現代 の石工の親方と見に行ったことがある。下から見上げたその石橋の下で、 僕等は息を呑んだ。一言｢すごい｣と石工は言った。あの石の勾配は、 知恵のないものには作れない。それが暗黙のうちに伝わってくる。 もう一度行きたいと思っている。 楕円上のある点において、その点と焦点が作る角度の両側に、相等しい角度を作る直線が接線である。 接線とは、｢ある曲線の1点近傍において、その1点のみ共有する直線｣である。 幾何証明において、補助点、補助線をいかに引くかがポイントである。 楕円の焦点は、正にその補助点である。楕円上の1点から直線は何本でも 引ける。だが、接線と呼べるものは多くない。キッチリと作画を繰り返す と、その定理が浮かび上がってくる。職人の棟梁は、その原理を頭の中 にたたき込んでいた。他人には教えない。秘伝である。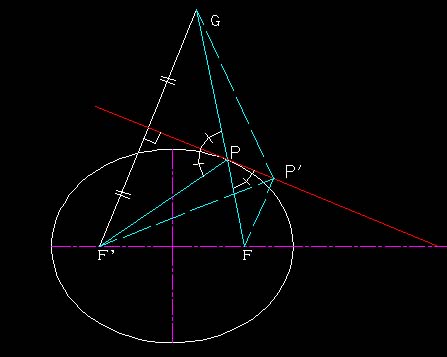  上に作画した直線が、楕円とただ1点で接することを証明する。 ということは、｢直線上の他のいかなる点も楕円上の点ではない｣ことを 証明するればよい。 証明 補助線ＧＦは点Ｐで楕円と交わりＧＰＦは直線である。 なぜなら、交角が等しい。さらに、Ｆ’Ｐ+ＰＦ＝ＧＰ+ＰＦ＝２ａ 接線の直線上の他の点に対して、同じように作画した ＧＰ’Ｆは、1直線とならない。なぜなら交角が等しくない。ＧＰ’Ｆの距離の合計はつねに2aより大である。したがって、この直線上の他のすべての点は楕円上の点ではない。
結論この直線は楕円上の点Ｐの接線である。
|
| 楕円の接線関数を調べてみる。 この式を１回微分する。 これが楕円の接線の勾配である。物理的意味は、接線と水平軸の角度 ω の タンジェントである。x , y を極座標で表現して整理する。 |
| 地球は回転楕円体とモデル化される。x y の数学座標平面を子午線面
に立てたと考えればいい。南北の軸回りに楕円を回転させてできる
立体ということになる。地球を水平面スライスすると、どこでも円ではある訳だ。三次元地球座標では極北軸を z とするので、いままでの ｘ をｚ に読みかえる必要はある。楕円の中心が地球の中心。三次元地球座標の原点と
なる。 2000年に、日本は回転楕円体モデルを100年続いたベッセルから ＧＲＳ80に変更した。近年の衛星測量の成果と整合を図るためであった。 海水平面をモデル化した面をジオイドと呼ぶ。重力場の等ポテンシャル面 という物理的意味がある。このジオイド面に一番近い回転楕円体がＧＲＳ80ということである。 水平ということは、このジオイド面の接線方向である。重力はこの面に 直角に働く。ところうが、地球全体としては回転楕円体であり、重力線は 延長すると座標原点には向かない。正確に地球中心に向くのは赤道面と 南北極点のみとなる。 大地の上で行う測量は、重力に対して角度を計測する。測量機械は 重力方向に、すなわち鉛直方向にセットするように出来ている。三角点といわれる重要な基準点は、衛星測量で計測されているのでいいのだが、 局地測量はこの光学機械で行う。測量における緯度は測地緯度と呼ばれる。 回転楕円体面に直角方向の角度である。地図の緯度は測地緯度である。三次元地球座標を極座表示した場合の角度、緯度ではない。  測地緯度 θ を用いた三次元地球座標の式を確認しておく。上図の 長さＮを誘導する。 
|
| 国土地理院のホームページには測地成果2000の資料が公開されています。新旧座標変換、ＢＬＸＹ変換のプログラムも公開されています。 数値地図のコンバーターを作成するにあたり、自作プログラムの 中に変換式を組み込まなければなりませんでした。国土地理院の資料 を参考にプログラムいたしました。その際、座標の考え方と 計算式を確認する意味で追計算しました。100年に一度の大改訂 ですので考え方を点検しておくことが必要でした。 私のような町の測量屋は公共座標網の中で仕事をしております。 三角点設置は業務の範囲の外であります。久しぶりに学生時代の 教科書を開いてみました。そもそも局地測量を中心とする 大学の教科書には参考にすべきページも多くありません。 ｢天文緯度と測地緯度｣。あれ、そんなのあった？。これが実情 です。 静かに開けた21世紀。しかし、静かに大転換が進行していた訳です。 学生時代の教科書の｢経緯度測量｣のページに、｢この項は歴史的記述となったため取り扱い注意｣と書き添えてページを閉じました。 感慨深い思いでした。 |